How do you teach the distributive property? When planning lessons, be sure you are maintaining perspective. Ask: What have your students already experienced with the content? This is particularly critical when students have gaps and require support to bridge that gap. You will need to have the perspective of how the related content has developed over the years/courses so that you can replicate that progression for struggling students via individualized learning. Ask: What leaps will your students make in upcoming courses that stem from what you do with the content now? It is important to identify future learning so that you can ensure adequate depth in your course. Let's review the progression of the distributive property...
 |
| 3.OA.B.5 |
In Grade 3, students use the distributive property as a strategy for multiplying. This is the concept builder for the distributive property. If students were unsuccessful when working strictly with numbers, then their efforts in applications with variables will be a stretch at best. Or worse yet...what if students memorized multiplication facts and never made sense of the concept through the distributive property?!?
 |
| 6.EE.B.5 |
In Grade 6, students use the distributive property to produce equivalent expressions. Notice the example includes using the distributive property to toggle between factored form (the result from division) and expanded form (the result from multiplication).
 |
| 7.EE.A.1 |
In Grade 7, students continue with the same concepts learned in Grade 6 with an extension to using rational numbers. Should 7th graders be solving equations that require using the distributive property? Continue reading.
 |
| 8.EE.C.7b |
In Grade 8 (and Accelerated MATH-7), students will use the distributive property to solve linear equations with rational coefficients. Notice the standard says "whose solutions
REQUIRE expanding expressions using the distributive property..." in order to solve the linear equation.
.png) |
| Differentiate the necessity of the distributive property. |
Perhaps MATH-7 students should be asked to solve equations that are similar to the equation in the left column above; however, this begs the question "How do we hope students solve that type of equation?". We also hope MATH-8 students recognize the need for the distributive property before they start the process of solving equations that are similar to the equation in the right column above.
This discussion highlights the Common Core State Standards 7.EE.A.1 and 8.EE.C.7b included in MATH-7, MATH-8 and Accelerated MATH-7.




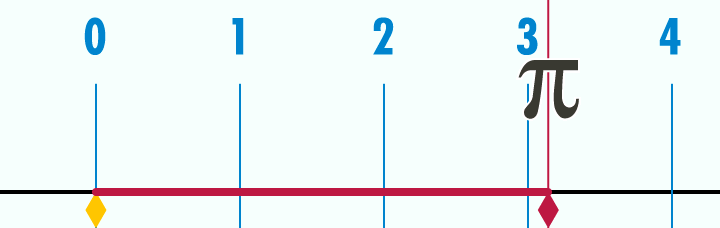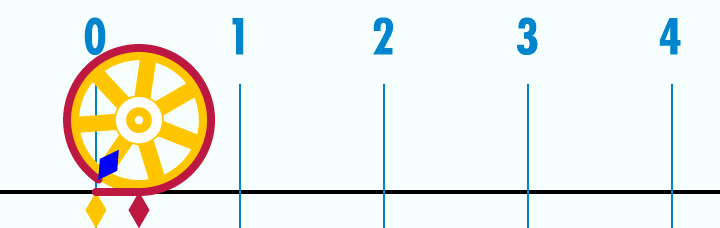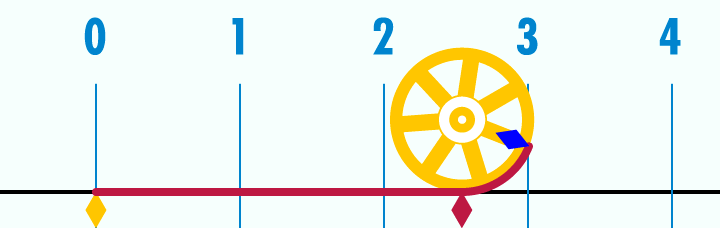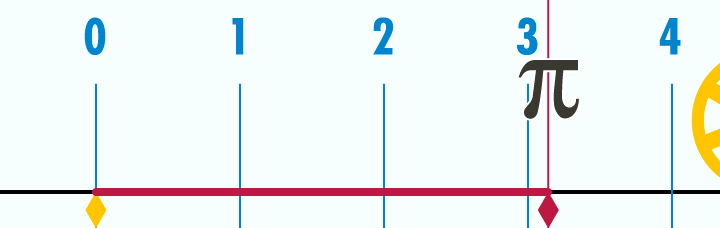

+Title+Pic.jpg)









.png)
